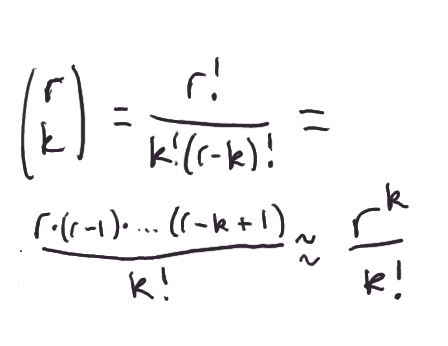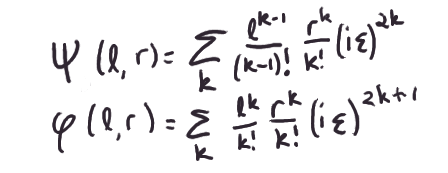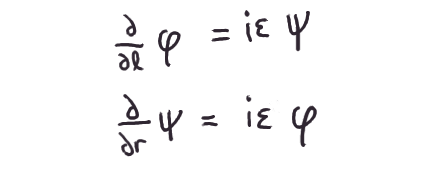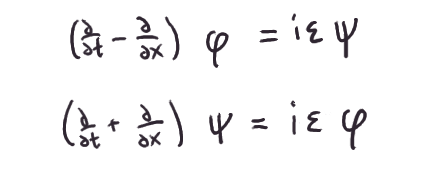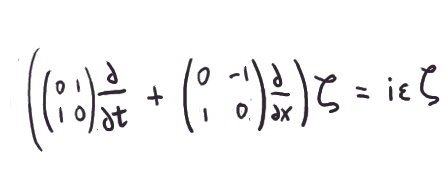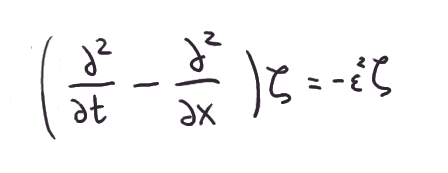From pebbles to electrons
Based on a paper by Kauffman and Noyes.
Part I: From pebbles to combinatorics
Here's a very boring zero-player game. Take a triangular tableau of little pits, kind of like a mancala board:
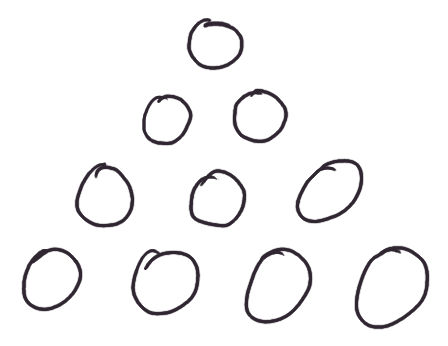Put a pebble in the top one:
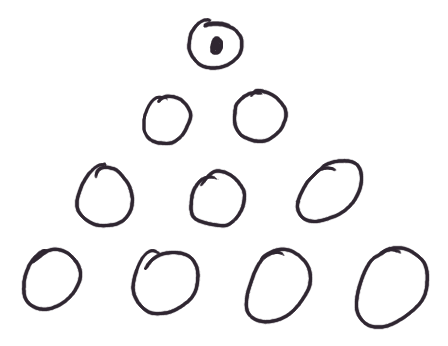And for every pebble you have, put one in each of the two pits immediately below it:
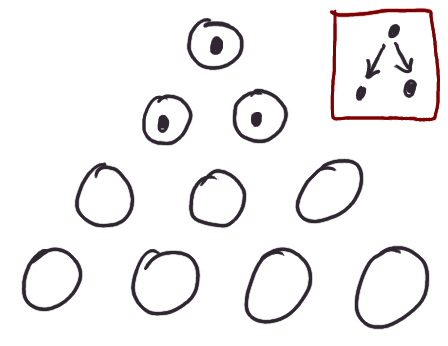Continue applying this rule all the way down:
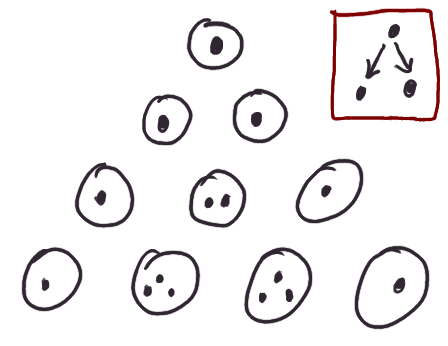Congratulations, you have just invented Pascal's Triangle, and
confronted the ineffable mysteries of probability and combinatorics.
Of course, we might have decided to have different kinds of pebbles, and different
rules for them. Perhaps a black pebble begets a green to the left, and
a black to the right, and a green pebble begets a black pebble to the
right, like so:
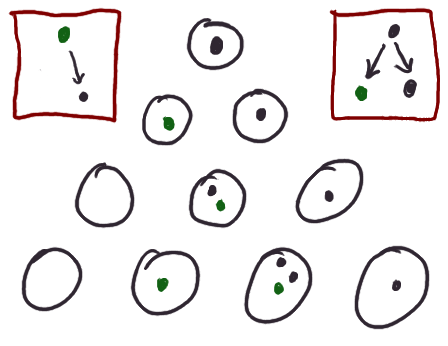And since today we are bold Mathematicians, we are comfortable employing
other, more general notions of number. Below, a green pebble begets one-half of
a black pebble to the right.
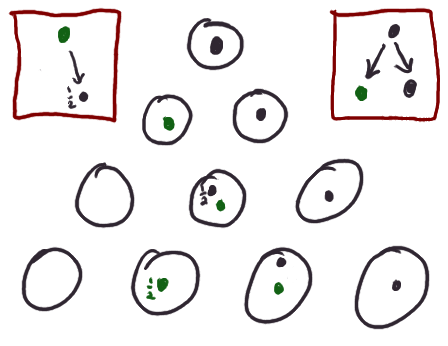Notice how the half-a-black-pebble that appeared upon the tableau
works: it generated half of a green to its left, and half of a black
to its right (which combined with another half-a-black that came from the green pebble in the same bin as the original half-a-black, formed a full black pebble...). This is only natural: it has half the effect of a full
black pebble.
But fractions are kids' stuff. The ghost of Richard Feynman appears,
and suggests
we consider
the following game. A black pebble begets a black pebble to its
right, but also a small imaginary amount of green pebbles, iε
of them, for ε a small fixed real number. A green pebble begets,
to its left, a green pebble and also iε black pebbles.
It's as if black pebbles long only to travel right, and green pebbles
to the left, but with a small --- and imaginary! --- probability, they
change their mind, and become the other kind of particle. Ahem,
pebble.
We would like to know how many pebbles we can expect to have in the
distant future at a particular place in the triangular tableau.
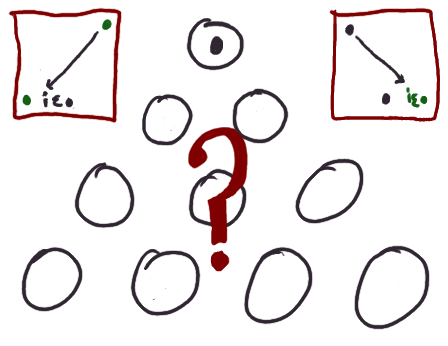Feynman's ghost, still hanging around for some reason, points out we
can compute this by summing over all paths through
the tableau to that place, letting each path contribute
(iε)d to the sum, where d is the number of times
that path changed direction.
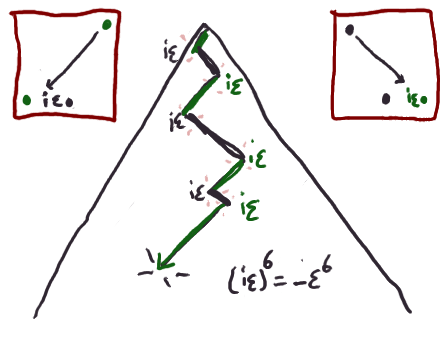We can work out an explicit formula by staring at the following
diagram, and doing our best to pretend that we are not just Mathematicians,
but Combinatorialists at that.
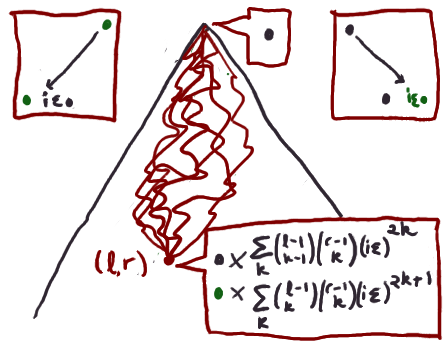
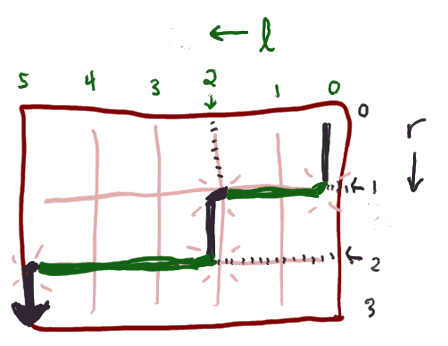Consider a path that travels a total of l hops down and to the
left, and r hops down and to the right, and starts out and ends up
going to the right. It's got to have an even number of kinks in it ---
say it has 2k of them --- and where they are can be completely
determined by a choice of k-1 places along the L-axis between 0 and l
(not inclusive) where kinks happen, and a choice of k places along the
R-axis between 0 and r (not inclusive) where kinks happen. The
corresponding formulae for paths that start and/or end by going to the
left are like so:
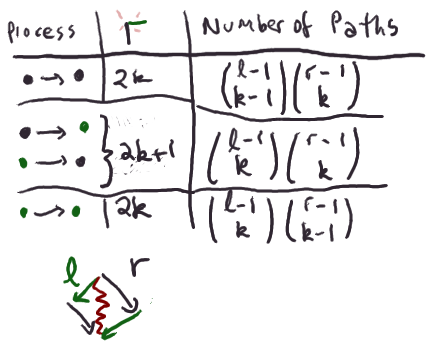And so we can return to the idea of summing over all possible paths by summing over k,
and throwing in the appropriate power of iε. Here's an explicit formula
for how many black and green pebbles you get at position (l,r),
if you start with one black pebble:
Part II: From combinatorics to electrons
What happens if r and l are really big? Then, for instance, the
difference between r and r-1 isn't really a big deal, among other
things. In fact, looking at the formula for r choose k, we can squinch
up our eyes and make the approximation:
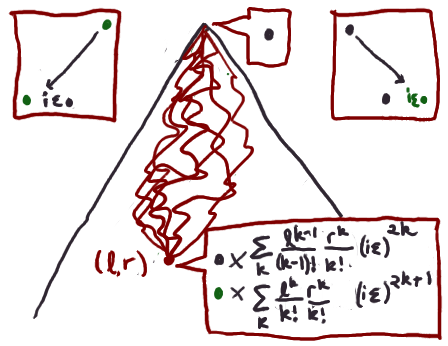
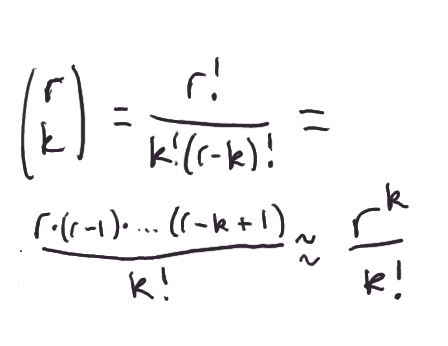Approximately, then, our explicit formula now looks like so:
Gosh, what a nice little power series in k. If we set
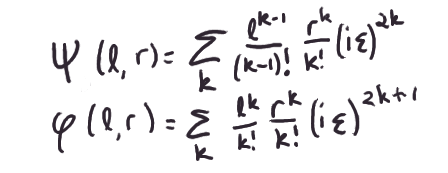then notice that we get some nice identities relating them:
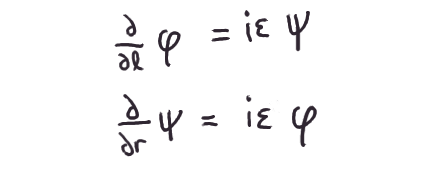
Furthermore remember that taking derivatives in the r and l
directions in spacetime actually correspond to differentiation
operations back in a more familiar coordinate system with a spatial
coordinate x and a time coordinate t:
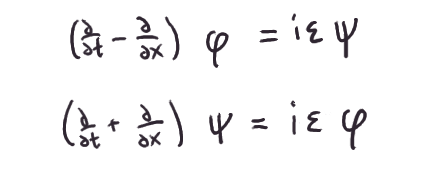What's crazy is that these two differential equations are saying that
our pebbles are electrons. Sort of. At least, electrons as conceived in a
mostly-broken early twentieth-century theory of special-relativistic
quantum mechanics, which, despite being mostly-broken, was still of
fantastic historical importance. They are the Dirac equation
for a 1d universe!
I'll massage it into a more familiar form:
Go back and look at the definitions and convince yourself that we just
said that if you start with a black pebble, the
wavefunction ahem pebble distribution you get can be thought of
as the following vector:
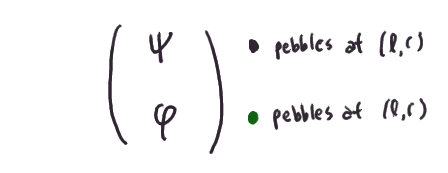Call this vector ζ. Then
the above equations above are equivalent to saying:
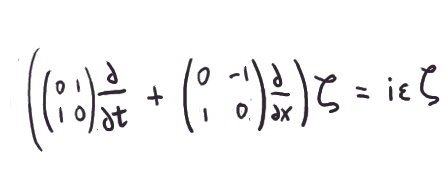All I did was express a pair of
equations as a single equation on vectors, via some clever choices of
matrices. By the way, everything I said up to now only dealt with
the situation where you start with a black pebble, but you'd arrive at the
same equation if you started with a green.
Anyhow, this is more or less the standard-looking Dirac equation.
There are anti-commuting matrices latching on to the time and space
derivatives on the left-hand-side. Over on the right we just have a
scalar times the overall wavefunction. That is, ζ is an
eigenfunction for that big operator that appears on the
left-hand-side, with eigenvalue iε. Well, if it is an
eigenfunction, there's no harm in hitting it with that
operator twice. If we do, the anticommuting matrices do their
magic and cancel out, and we're left with a version of
the Klein-Gordon
equation:
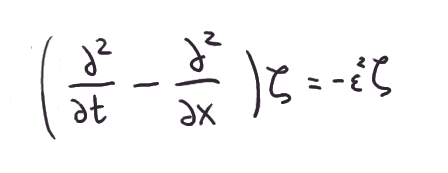Cribbing the definitions of the energy and momentum operators from
wikipedia, and deciding to interpret ε as the mass of our
particle, we get at last that lovely relationship among energy,
momentum, and mass from special relativity:
And that's just one Taylor-series-expansion-of-sqrt(p^2+m^2) away from
a very famous equation, indeed.
Not bad for a heap of imaginary pebbles!
Jul 12 2011