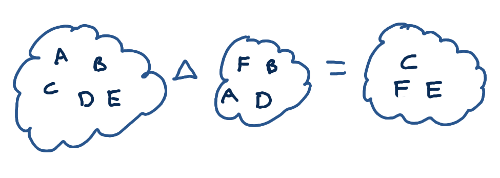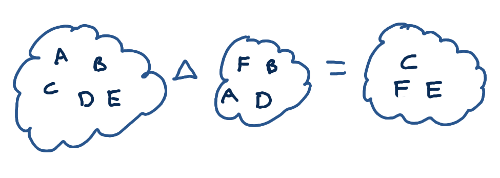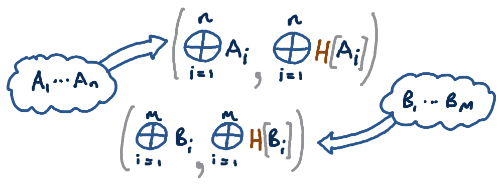So you have two sets, right, and you want to know their symmetric
difference --- that is, the set of things that's in one set and not
the other, or in the other set and not the one.
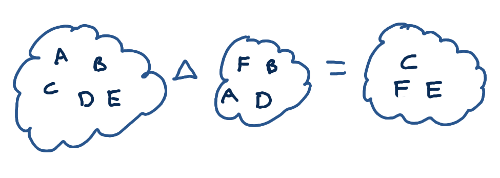 Not too bad. Just sort them, walk down both lists, and see where they differ.
However, you are unlucky today, and they are very big sets, in very
far away places.
Not too bad. Just sort them, walk down both lists, and see where they differ.
However, you are unlucky today, and they are very big sets, in very
far away places.
 Now simply comparing them element-by-element really sucks --- you have
to transmit every element across the wire to see if it exists at the
remote end! Oof, such wasted bandwidth. The only piece of good luck you have
is that, for some reason, you know they are very similar ---
that the size of their difference is small. What can you do, then?
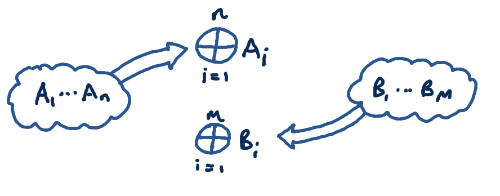
Well, your mind turns to checksumming. What happens if we take a big
XOR of all the elements of both lists, and only transmit that?
Now simply comparing them element-by-element really sucks --- you have
to transmit every element across the wire to see if it exists at the
remote end! Oof, such wasted bandwidth. The only piece of good luck you have
is that, for some reason, you know they are very similar ---
that the size of their difference is small. What can you do, then?
Well, your mind turns to checksumming. What happens if we take a big
XOR of all the elements of both lists, and only transmit that?
 This'll probably alert you whether the sets are different, at least.
Although it's not perfect. If one set is {1,2} and the other {3}, the checksum
will lie to you and tell you they're the same set, even though they're not.
Let's transmit a checksum of hashes of all the elements as well.
Pick your favorite hash function H, and do:
This'll probably alert you whether the sets are different, at least.
Although it's not perfect. If one set is {1,2} and the other {3}, the checksum
will lie to you and tell you they're the same set, even though they're not.
Let's transmit a checksum of hashes of all the elements as well.
Pick your favorite hash function H, and do:
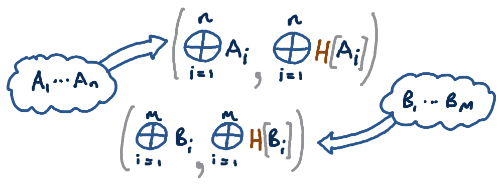 Ok, great. This is a pretty reliable measure of whether the
sets are different --- that is, whether the symmetric difference is
nonempty or not --- and, even better, in the event that they differ
by exactly one element, we can reliably detect that, and recover what
that element was! Make the abbreviations:
\[s_A = \bigoplus_{i=1}^n A_i \qquad s_B = \bigoplus_{i=1}^m B_i\]
\[h_A = \bigoplus_{i=1}^n H[A_i] \qquad h_B = \bigoplus_{i=1}^m H[B_i]\]
These are the only four chunks of data sent across the wire. Or, actually,
we only need to send two of them: either the person holding the A-database sends \(s_A\) and \(h_A\) to the person holding the B-database (who just
computes \(s_B\) and \(h_B\) herself) or the other way around.
In any event, take a look at whether
\[H(s_A \oplus s_B) = h_A \oplus h_B\]
I claim this can only happen if the difference-set \(D =
\{A_1,\ldots,A_n\} \triangle \{B_1,\ldots,B_m\}\) has size one.
This is because
\[ s_A \oplus s_B = \bigoplus_{x\in D} x\]
\[ h_A \oplus h_B = \bigoplus_{x\in D} H(x)\]
and you're only going to find that
\[ H\left( \bigoplus_{x\in D} x\right) =
\bigoplus_{x\in D} H(x)\]
if \(D\) is a singleton (or empty!). And when this does happen,
the missing element we're interested in is just \(s_A \oplus s_B\).
Ok, great. This is a pretty reliable measure of whether the
sets are different --- that is, whether the symmetric difference is
nonempty or not --- and, even better, in the event that they differ
by exactly one element, we can reliably detect that, and recover what
that element was! Make the abbreviations:
\[s_A = \bigoplus_{i=1}^n A_i \qquad s_B = \bigoplus_{i=1}^m B_i\]
\[h_A = \bigoplus_{i=1}^n H[A_i] \qquad h_B = \bigoplus_{i=1}^m H[B_i]\]
These are the only four chunks of data sent across the wire. Or, actually,
we only need to send two of them: either the person holding the A-database sends \(s_A\) and \(h_A\) to the person holding the B-database (who just
computes \(s_B\) and \(h_B\) herself) or the other way around.
In any event, take a look at whether
\[H(s_A \oplus s_B) = h_A \oplus h_B\]
I claim this can only happen if the difference-set \(D =
\{A_1,\ldots,A_n\} \triangle \{B_1,\ldots,B_m\}\) has size one.
This is because
\[ s_A \oplus s_B = \bigoplus_{x\in D} x\]
\[ h_A \oplus h_B = \bigoplus_{x\in D} H(x)\]
and you're only going to find that
\[ H\left( \bigoplus_{x\in D} x\right) =
\bigoplus_{x\in D} H(x)\]
if \(D\) is a singleton (or empty!). And when this does happen,
the missing element we're interested in is just \(s_A \oplus s_B\).
How do we recover more than one differing element?
A recent paper by Eppstein, Goodrich, Uyeda, and Varghese gives a really
neat way of doing it, by
throwing a clever variant of Bloom filters at the problem. (There is
a longer trail in the literature than just this paper, but this
is the algorithm that I feel like talking about right now!)
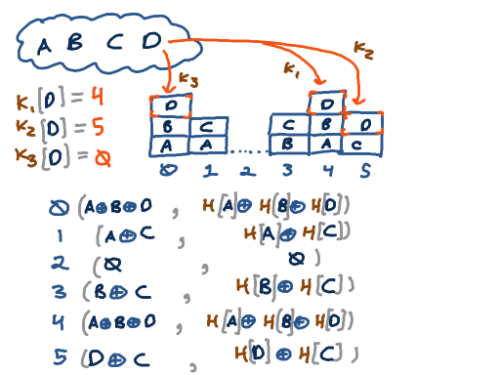
Pick a few more of your favorite hash functions, say \(p\) of them,
call them \(K_1,K_2,\ldots,K_p\),
whose range is rather small: \(0\ldots b-1\) for some number of buckets \(b\).
These hash functions assign set-elements to buckets, but redundantly by a factor of \(p\). Here's a picture for \(p=3\) and \(b = 6\):
 For every bucket we do the same kind of checksumming calculation that
we did before, taking a big XOR of all the elements that ended up in
that bucket, and a big XOR of the hashes of those elements. We
transmit \(2p\) numbers across the wire.
For every bucket we do the same kind of checksumming calculation that
we did before, taking a big XOR of all the elements that ended up in
that bucket, and a big XOR of the hashes of those elements. We
transmit \(2p\) numbers across the wire.
To actually find the set difference, we
do the same sort of XOR-everything-in-sight, but this time bucket-by-bucket,
and look at what's left.
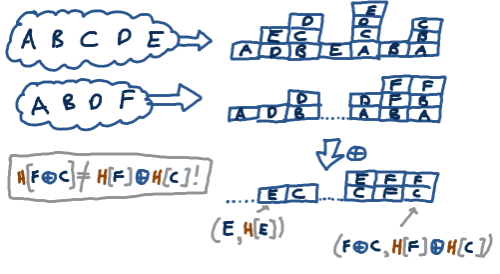 If we're lucky, some bucket will
contain just one differing element after most of the sets' elements in
that bucket cancel out. For instance, in bucket #1, the Ds cancel out
and we're left with \(E\) and \(H[E]\). In bucket #2, the Bs and Ds
cancel out and we're left with \(C\) and \(H[C]\). And in these
cases we can reliably check that the hash-of-differences is the
difference-of-hashes to see that we have exactly one element, just as
we did above.
If we're lucky, some bucket will
contain just one differing element after most of the sets' elements in
that bucket cancel out. For instance, in bucket #1, the Ds cancel out
and we're left with \(E\) and \(H[E]\). In bucket #2, the Bs and Ds
cancel out and we're left with \(C\) and \(H[C]\). And in these
cases we can reliably check that the hash-of-differences is the
difference-of-hashes to see that we have exactly one element, just as
we did above.
The thing that I found really clever is the observation that once
you get an element that you know is in the symmetric difference
of the original two sets, you know all the p things it hashes
to, so you can wipe them out and make even more progress. Once we find
\(C\), we can cancel out the \(C\) in bucket 5, which leaves just an \(F\),
which we were unable to notice before, since \(H[F\oplus C] \ne H[F]\oplus H[C]\).
So it turns out we have very good odds of succeeding at
stubbornly unravelling the loose thread in the sweater, and recovering
the exact set of elements in symmetric difference, as long as
\(b\) is at least about 1.5 times the size of the difference, and
\(p\) is ideally about 3 or 4. The theory behind these numbers is
calculating the probability that a random hypergraph of uniform
degree \(p\) with \(|D|\) edges and \(b\) vertices has an empty 2-core.
This also has some fascinating connections to phase transitions
in randomly-created SAT problems --- a topic for another time, maybe.