Say you're trying to do the integral: \[ \int\limits_{-\infty}^\infty e^{-Ax^2 + Bx + Cx^3}dx \] Well... this looks an awful lot like \[ \int\limits_{-\infty}^\infty e^{-Ax^2 + Bx}dx \] which can be solved by more conventional means: you complete the square \[e^{B^2/4A}\int\limits_{-\infty}^\infty e^{-Ax^2 + Bx - (B^2/4A)}dx\] \[= e^{B^2/4A}\int\limits_{-\infty}^\infty e^{-(\sqrt Ax +B/2\sqrt A)^2}dx\] do a substitution \(u = \sqrt Ax +B/2\sqrt A\) to get \[e^{B^2/4A}\int\limits_{-\infty}^\infty (1/\sqrt{A})e^{-u^2}du =\sqrt{\frac{\pi}{A}} e^{B^2/4A}\] (You get \(\int e^{-u^2} du = \sqrt\pi\) via a cute trick that passes through polar coordinates)

However, we still have that pesky \(Cx^3\) bit there. What do we do about it? Let's think like physicists. The little physicist on our shoulder says: when in doubt, expand as a power series. Our original integral is equal to: \[\int\limits_{-\infty}^\infty e^{-Ax^2 + Bx}\left(\sum_{n=0}^\infty \frac{(Cx^3)^n}{n!} \right)\,dx\] Well, okay, now we've got mere \(x^{3n}\)s where once we had scary \(e^{x^3}\)s. That feels like progress, although we still can't pull this out of the integral because it still involves \(x\). Say... hitting that particlar exponential expression we have there by \(d/dB\) has the same effect as multiplying by \(x\), though. Even if we do it multiple times! That is, \[ (d/dB)^m (e^{-Ax^2 + Bx}) = x^m (e^{-Ax^2 + Bx})\] for any m. Therefore \[\int\limits_{-\infty}^\infty e^{-Ax^2 + Bx}\left(\sum_{n=0}^\infty \frac{(Cx^3)^n}{n!} \right)\,dx = \int\limits_{-\infty}^\infty \sum_{n=0}^\infty\frac{C^n}{n!}(d/dB)^{3n} (e^{-Ax^2 + Bx}) \] and now we can swap the sum and integral and pull all that junk outside the integral sign, since it's all linear and doesn't depend on \(x\). \[=\sum_{n=0}^\infty \frac{C^n}{n!}(d/dB)^{3n}\int\limits_{-\infty}^\infty e^{-Ax^2 + Bx} \] And we can solve the integral we know how to solve: \[= \sum_{n=0}^\infty \frac{C^n}{n!}(d/dB)^{3n} \sqrt{\frac{\pi}{A}} e^{B^2/4A}\] \[=\sqrt{\frac{\pi}{A}} \sum_{n=0}^\infty \frac{C^n}{n!}(d/dB)^{3n} e^{B^2/4A}\] In some sense, we're done now. We could have Mathematica or whatever chug away computing the \(3n^{th}\) derivative of \(e^{B^2/4A}\) and compute this value to whatever accuracy we want, without having to resort to Riemann sums of the original integral, yuck. But let's look closer at what \[ (C^n/n!)(d/dB)^{3n} e^{B^2/4A}\] really means.

Better yet, let's just look at \[ (d/dB)^{m} e^{B^2/4A}\] for the first view values of \(m\).

\(m\)	\((d/dB)^{m} e^{B^2/4A}\)
0	\(e^{B^2/4A}\)
1	\((B/2A) e^{B^2/4A}\)
2	\((1/2A + B^2/4A^2) e^{B^2/4A}\)

Hmm. Well, obviously every one of these is going to have \(e^{B^2/4A}\) in it, and moreover I'm going to get sick of writing powers of \(1/2A\). So let's abbreviate \( V = e^{B^2/4A}\) and \(Q = 1/2A\). Then we get

\(m\)	\((d/dB)^{m} V\)
0	\(V\)
1	\((BQ) V\)
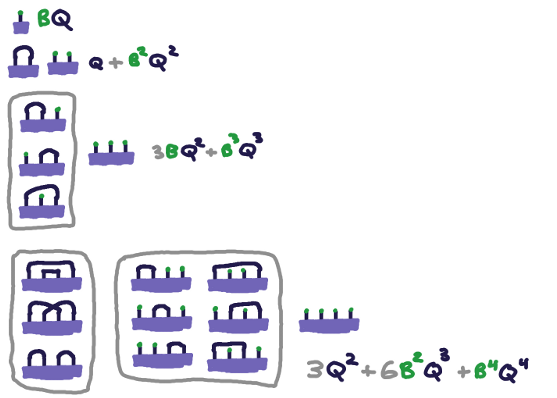
2	\((Q + B^2Q^2) V\)
3	\((3BQ^2 + B^3Q^3) V\)
4	\((3Q^2 + 6B^2Q^3 + B^4Q^4) V\)
...	...

What's the recurrence going on here? If \(F\) is any old function, and we hit \(FV\) with \(d/dB\), we get \[(dF/dB)V + F(dV/dB) \] \[= ((dF/dB) + (BQ)F)V\] So ignoring the \(V\) that's off to the side, it's like we're repeatedly hitting an expression with the linear operator \[d/dB + BQ\] which means "take your function differentiated by \(B\), and take your original function multiplied by \(BQ\), and add them together." In a table:

\(m\)	\((d/dB + BQ)^m (1)\)
0	\(1\)
1	\(BQ\)
2	\(Q + B^2Q^2\)
3	\(3BQ^2 + B^3Q^3\)
4	\(3Q^2 + 6B^2Q^3 + B^4Q^4\)
...	...

Here's a very strange fact: the \(m\)th row of this table is actually giving us a sort of census of wiring diagrams with \(m\) sockets. Watch this:

The coefficient of \(B^iQ^j\) that appears in \((d/dB + BQ)^m (1)\) is the number of wiring diagrams with m sockets, i dangling wire-ends, and j total wires. The differential operator \((d/dB + BQ)\) is telling us what to do when we add a new socket: either we connect up a previously-existing dangling wire end to this socket (\(d/dB\)) or we make up a new wire and wire-end (\(BQ\)).

And now finally we can tell a bit of the story of \[ (C^n/n!)(d/dB)^{3n} e^{B^2/4A}\] It asks for wiring diagrams with multiples of three sockets, and has a symmetry factor of \(1/n!\) that says that rearrangements of the 3-socket groups doesn't matter. Here's a picture of all of the \(C\) contributions to the infinite sum and just a small selection of the \(C^2\)s:

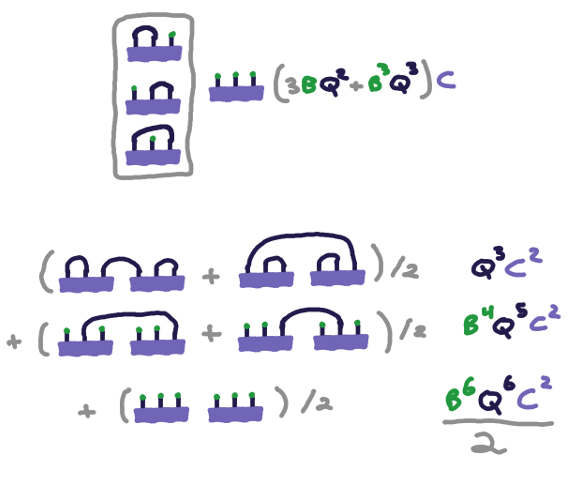
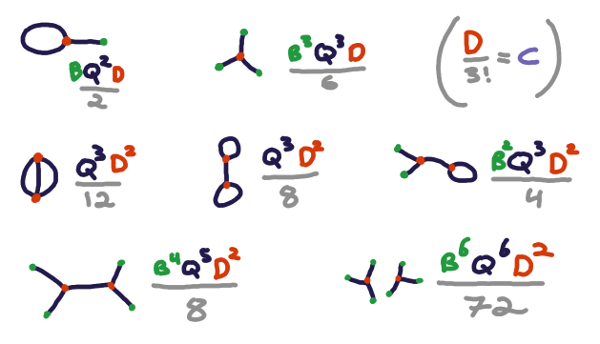
Diagrams that are to some extent symmetric under rearrangement of socket-groups 'count less' in the grand scheme of things. The bottommost of the five \(C^2\) diagrams above has this property. It has no distinct partner obtained by swapping the three socket-groups, and so counts for only 1/2 of a diagram.

If you're really comfortable with this groupoid cardinality symmetry-factor accounting nonsense, you can decide that you wanted \(C\) to be of the form \(D/3!\) for some 6-fold larger constant \(D\) in the first place, to account for all possible permutations of sockets within a socket-block as well, with the same proviso of more-symmetric diagrams (for this new notion of symmetry) 'counting less'. In that case, the diagrams are more naturally depicted not as wires going into an ordered list of sockets in a block, but as wires freely going into degree-3 vertices in a graph. These are Feynman diagrams! Here's another (nonexhaustive) pile of interesting examples:

The number in the denominator of each of these --- the symmetry factor --- is basically the number of graph automorphisms of the diagram. The exact meaning of flipping around edges gets me a bit confused, still. When in doubt I go back to the explicit socket diagrams and work out how many labelled diagrams there are, and divide by enough 3!s to account for all the \(D\)s.

And the sum of all of these diagrams, times \(\sqrt{\frac{\pi}{A}} e^{B^2/4A}\), is the value of the integral \[\int\limits_{-\infty}^\infty e^{-Ax^2 + Bx + Cx^3}dx\] that we started with.

...Right? Well, we've been sloppy about treating convergence of anything this whole time. Actually, if \(C\) is positive, then \(e^{Cx^3}\) blows up to infinity in the positive \(x\) direction faster than \(e^{-Ax^2}\) can tame it, and if \(C\) is negative, it blows up in the negative \(x\) direction. I guess this might have something to do with why many textbooks I've seen treat "the \(\phi^4\) theory" rather than the "the \(\phi^3\)"? I'm not actually sure. Anyhow, I could make a convergent integral by having \(-x^4\) in there instead of \(x^3\), and then there would be degree-4 vertices instead of degree-3.

It seems to my gut sense strangely likely that the infinite series of diagrams should converge, however, even for the degree-3 case, as long as \(D\) is small. But maybe I'm wrong about that, and the combinatorial explosion of graphs grows faster than increasing powers of \(D\).