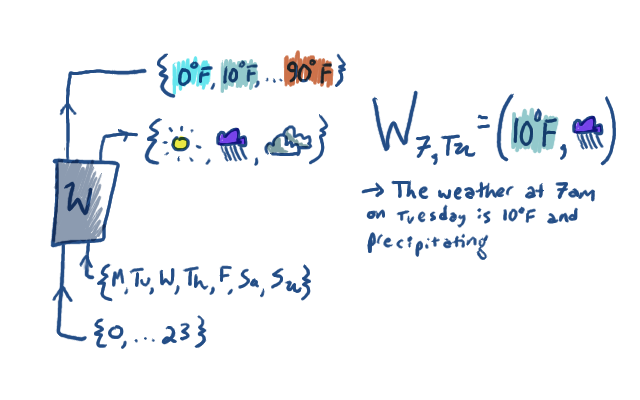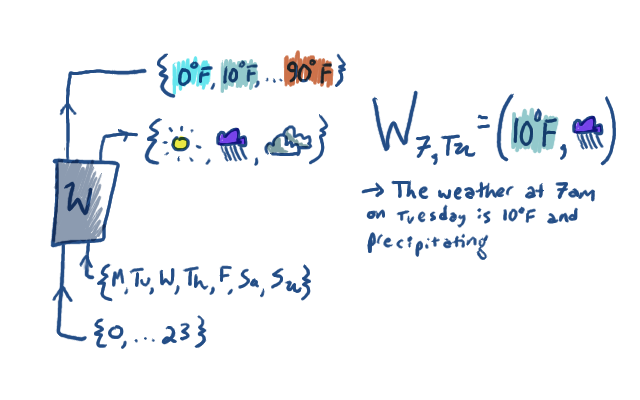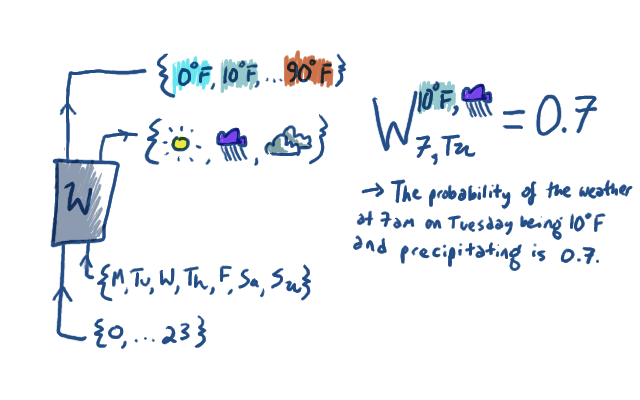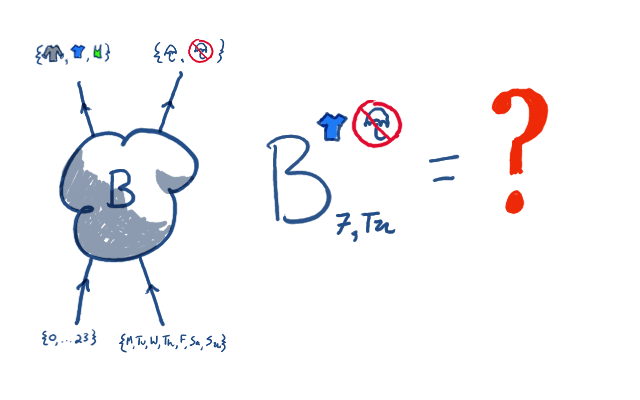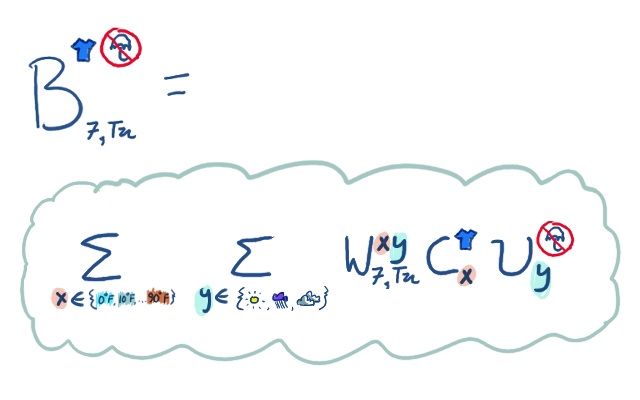Imagine a function W that is supposed to predict the weather. It takes
in a time-of-day (represented as a number 0 through 23) and a day of
the week, and outputs a prediction of temperature (between 0 and 90
degrees, rounded to the nearest 10 degrees), and whether it will be
sunny, precipitating, or cloudy. It looks like this:
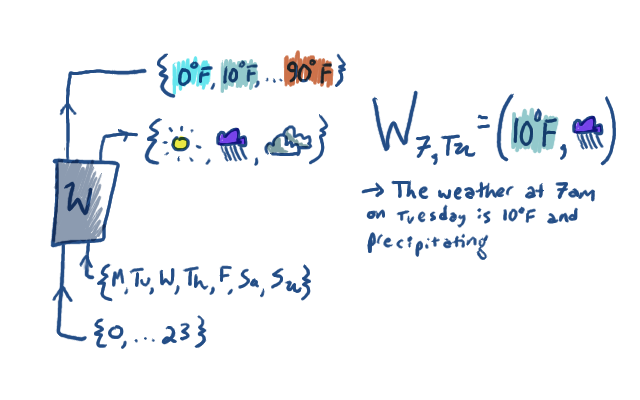This isn't too complicated. We all learned in kindergarten about
functions, and plugging values into them, and composing them, and how it's
associative, and so on.
To make things more interesting, we could imagine that it's a
randomized function. What information do we need to know about it now?
For every set of inputs and set of outputs, we want to know
the probability those outputs come out, given those inputs. The situation
looks like this, for example:
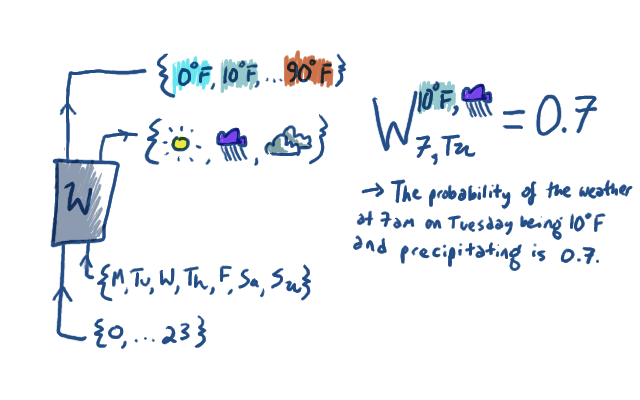I'm really depicting W twice, (as I did above) once pictorially, and once
in the more traditional "texty" way that is meant to be reminiscent of
tensor algebra. Also, all that's really depicted there is just one example
entry of W.
In the "texty" version, we put the outputs of the function as
superscripts on the W. They're clearly outputs in the sense that
they're the prediction, but you have to admit that they're
functioning kind of like inputs to W, too. If I give W its
input subscripts and output superscripts, then it gives me back a
probability. To fully specify the randomized function that is W, we
have to choose $24 \times 7 \times 10 \times 3$ probability numbers.
Anyhow, let's imagine a couple of other probabilistic functions:
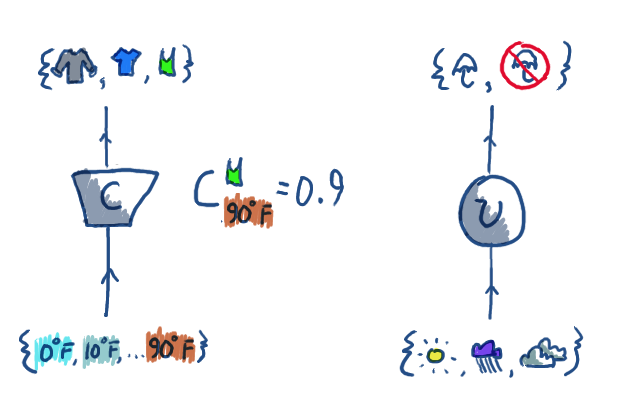Here I'm showing C pictorially and textually, and just giving U pictorially;
you should be able to fill in what a typical entry of U would look like.
C predicts what kind of clothing (sweater, tshirt, tank top) to wear
given the temperature. U predicts whether we'll take an umbrella is
needed, given the precipitation. To specify C, we need to give
$10\times 3$ probability numbers; probability of sweater given 0$^\circ F$,
probability of sweater given 10$^\circ F$, ... probability of tshirt given
0$^\circ F$, ... probability of tank top given 80$^\circ F$, probability
of tank top given 90$^\circ F$. To specify U, we need to give $3\times 2$ numbers.
We can compose randomized functions just like we can compose regular functions.
Here's a picture of combining the weather function with the clothing and umbrella functions:
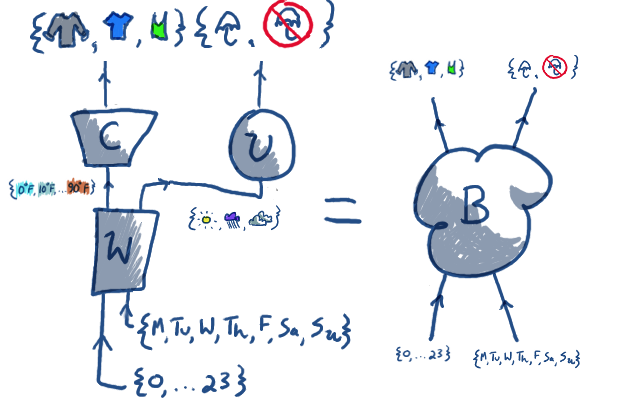We call the whole big mess "B". It's a randomized function from time and weekday
to clothing and umbrella-status. How can we actually compute probability
values for B? For instance, what's the probability that we wear a tshirt
and don't have an umbrella on Tuesday at 7am?
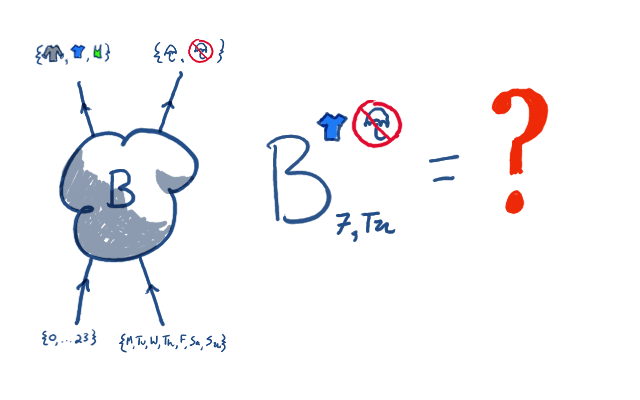Here I appeal to your intuitions about probabilities of things that
depend on other things. To find that probability, we have to consider
all the possibilities of what could happen with the weather,
and sum over them. The probability that we wear a tshirt
and don't have an umbrella on Tuesday at 7am is the sum over
all temperatures and weathers, of the probability of that temperature and
weather happening at Tuesday at 7am, times the probability
of wearing a tshirt given that temperature, time the probability
of having an umbrella given that weather. In a doodle, it looks like this:
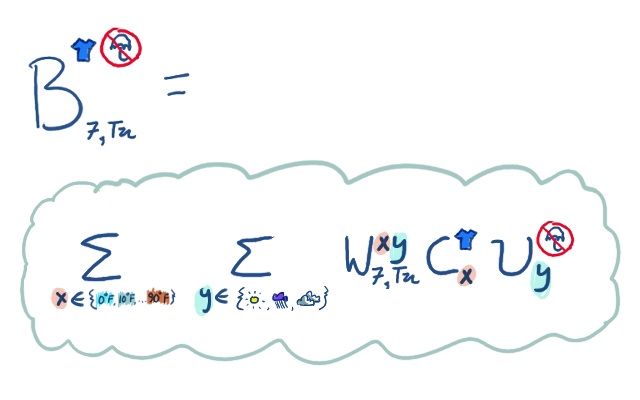This looks exactly like a tensor
contraction formula, because it is one. Each variable being summed
over corresponds to a 'wire' hooking up the input of some function to
the output of another. The variable therefore occurs once as a
superscript (output) and once as a subscript (input). This is why the Einstein
summation convention makes good sense.
The moral here is that in some sense "all tensors are" are little
probabilistic functions from a few inputs to a few outputs. The way in
which that is a lie is that real tensors are free to not satisfy a
couple of the axioms of probability! Their entries don't have to be
between 0 and 1, and they don't have to sum to 1 like probabilities
do. But their notion of input and output, and the way they compose are
very similar, and I find it very intuitively helpful to think about
the two as related.